
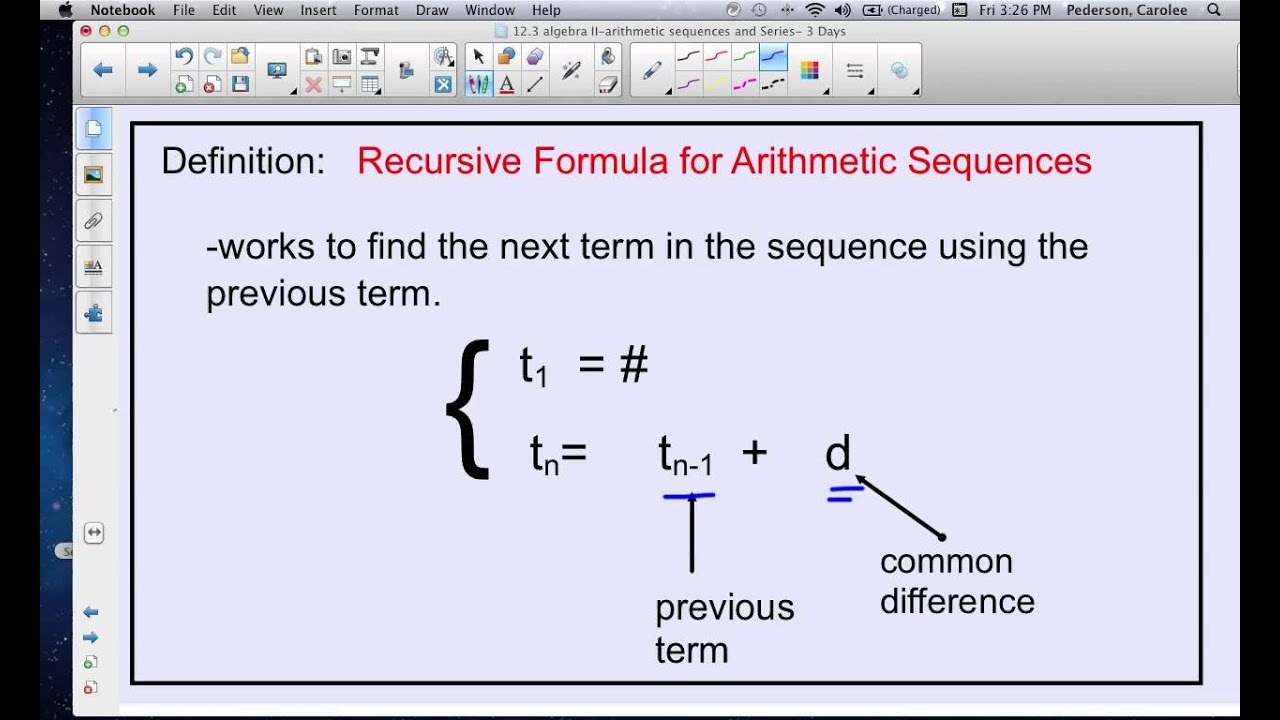
Writing Formulas for Arithmetic Sequences Sample QuestionsĪrithmetic sequences are found in many real-world scenarios, so it is useful to have an understanding of the topic. For example, in the sequence \(90,80,70…\) the common difference is \(-10\). A sequence can be increasing or decreasing, so the common difference can be positive or negative. This consistent value of change is referred to as the common difference. Formulas of Arithmetic Sequence an nth term that has to be found a1 1st term in the sequence n Number of terms d Common difference Sn Sum of n. For example, in the sequence \(10,13,16,19…\) three is added to each previous term. Each term in an arithmetic sequence is added or subtracted from the previous term.

Writing Formulas for Arithmetic Sequences OverviewĪn arithmetic sequence is a list of numbers that follow a definitive pattern. If the term-to-term rule for a sequence is to multiply or divide by the same number each time, it is called a geometric sequence, eg 3, 9, 27, 81, 243. If the position is \(n\), then this is \(2 \times n + 1\) which can be written as \(2n + 1\). To get from the position to the term, first multiply the position by 2 then add 1. Write out the 2 times tables and compare with each term in the sequence. In this sequence it's the 2 times tables.
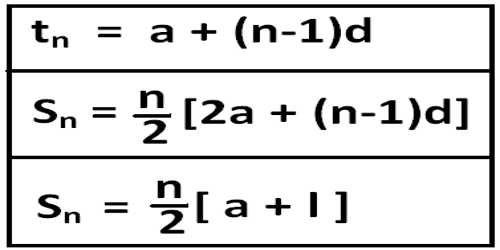
This common difference gives the times table used in the sequence and the first part of the position-to-term rule. In this case, there is a difference of 2 each time.

įirstly, write out the sequence and the positions of the terms.Īs there isn't a clear way of going from the position to the term, look for a common difference between the terms. Work out the \(nth\) term of the following sequence: 3, 5, 7, 9. If the position is \(n\), then the position to term rule is \(n + 4\). In this example, to get from the position to the term, take the position number and add 4 to the position number.
#Formulas for arithmetic sequences how to#
Next, work out how to go from the position to the term. įirst, write out the sequence and the positions of each term. Work out the position to term rule for the following sequence: 5, 6, 7, 8. The first five terms of the sequence: \(n^2 + 3n - 5\) are -1, 5, 13, 23, 35 Working out position-to-term rules for arithmetic sequences Example Write the first five terms of the sequence \(n^2 + 3n - 5\). (Notice how this is the same form as used for quadratic equations.) Any term of the quadratic sequence can be found by substituting for \(n\), like before. The \(nth\) term of a quadratic sequence has the form \(an^2 + bn + c\). \(5n − 1\) or \(-0.5n + 8.5\) are the position-to-term rules for the two examples above.Īrithmetic sequences are also known as linear sequences because, if you plot the position on a horizontal axis and the term on the vertical axis, you get a linear (straight line) graph. The position-to-term rule (or the \(nth\) term) of an arithmetic sequence is of the form \(an + b\). If the term-to-term rule for a sequence is to add or subtract the same number each time, it is called an arithmetic sequence, eg:Ĥ, 9, 14, 19, 24.


 0 kommentar(er)
0 kommentar(er)
